A.1 Electromagnetic Wave Propagation in a Dielectric Ring
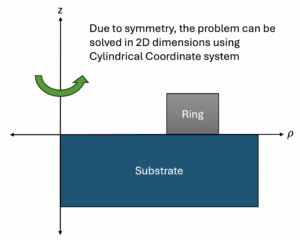
Goal: Development of a 2D code to calculate the characteristics of the TE and TM wave propagation inside a dielectric ring.
Dielectric ring resonators are crucial in photonics for their ability to confine and enhance light within compact structures, enabling high-precision filtering, sensing, and nonlinear optical processes essential for advanced photonic devices.

What We Need: To study TE and TM mode electromagnetic waves confined in a lossless dielectric ring, we need to develop a numerical solver based on the finite-element method (FEM) or finite-difference method (FDM). These methods allow us to discretize Maxwell’s equations in cylindrical coordinates, accommodating the curvature and boundary conditions specific to the ring resonator geometry. By meshing the dielectric ring structure with either triangular elements in FEM or a grid in FDM (easier than triangulation), the solver will numerically solve the eigenvalue problem associated with the wave equation, yielding the resonant frequencies and corresponding field distributions of the TE and TM modes.
References:
- Funaro, Daniele. 2020. “Electromagnetic Waves in Annular Regions” Applied Sciences 10, no. 5: 1780. https://doi.org/10.3390/app10051780
- Sadiku, Numerical Techniques in EM, 3rd Edition, chapter 3, section 10 (for finite differencing in cylindrical coordinate system)
Future Work: The solver can be optimized for high accuracy by refining the mesh near the dielectric interfaces where field gradients are steepest, and by incorporating perfectly matched layers (PML) or absorbing boundary conditions to minimize reflections and emulate an open system. This approach provides a powerful tool for analyzing the modal characteristics of dielectric ring resonators, facilitating the design and optimization of photonic devices.
A.2 “Forward: Go – Backward: No” Medium Design with the Adjoint Method
Main Research Question: Can we use the adjoint method and design a medium, which would allow electromagnetic waves to propagate though in one direction but stop them in the opposite direction?
Inverse photonic design refers to the process of designing a photonic structure with specific desired properties or functionalities. This can be quite challenging, as designing a structure to achieve a certain optical behavior often involves a complex interplay of various parameters, such as geometry, refractive indices, and other material properties.
The adjoint method is a mathematical technique used in optimization and sensitivity analysis. It is particularly useful when dealing with problems that involve the optimization of a scalar function with respect to a set of parameters. In the context of inverse photonic design, the adjoint method is used to efficiently calculate the gradient of a desired objective function (e.g., maximizing light absorption, minimizing reflectance) with respect to the design parameters of a photonic structure. A typical workflow for the adjoint method is provided in the box below.
So far, researchers have successfully implemented the adjoint method for the design of multilayered media with desired reflection and transmission characteristics, resonators, beam splitters, etc. This project aims to design a film with transmittance in one direction that is at least 10 times stronger than in the opposite direction.
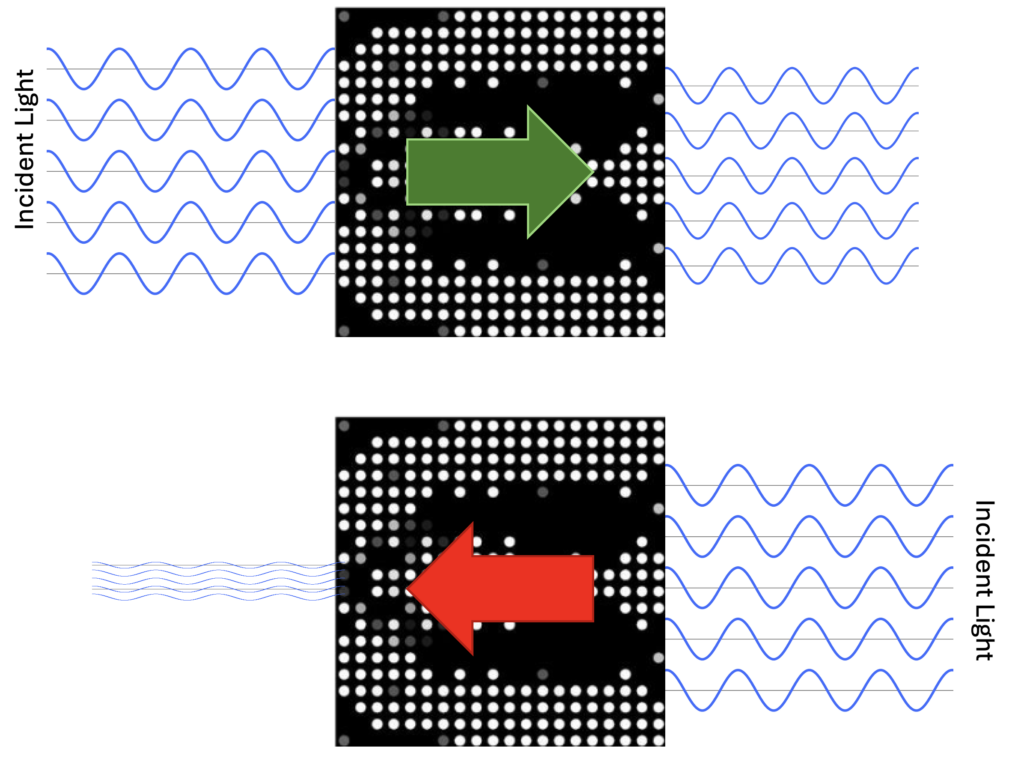
The adjoint method is particularly valuable in inverse photonic design because it allows you to efficiently compute the gradient of the objective function with respect to a large number of design parameters. This is crucial when dealing with complex and high-dimensional design spaces that are common in photonic structures. It helps rapidly converge toward optimal designs that fulfill specific optical requirements. |
Minimum Requirements:
- Intermediate knowledge of Python (both data structures and algorithms)
- Good understanding of vector calculus
Preferred Skills:
- Familiarity with FDTD or FDFD methods
- Experience in numerical optimization
A.3 Image Classification Through an Adjoint Optimized Unit
Main Research Question: Can we design a structure that can classify the images using light?
The adjoint method is a mathematical technique used in optimization and sensitivity analysis. It is particularly useful when dealing with problems that involve the optimization of a scalar function with respect to a set of parameters. In the context of inverse photonic design, the adjoint method is used to efficiently calculate the gradient of a desired objective function (e.g., maximizing light absorption, minimizing reflectance) with respect to the design parameters of a photonic structure.
For example, the figure below shows an adjoint-optimized structure that splits the pulses based on their polarization. If the excitation is TE polarized, then it leaves the structures from the lower branch on the right. If it is TM polarized, then it leaves the structure from the upper branch.
 Figure 1 a) An adjoint-optimized beam-splitter, b) and c) show how TE and TM pulses propagate through this structure, respectively [1].
Figure 1 a) An adjoint-optimized beam-splitter, b) and c) show how TE and TM pulses propagate through this structure, respectively [1].
The goal of this project is to design a unit with the adjoint method that will be excited with the light that passes through an image of a number and output light from the corresponding branch, as shown in Figure 2.
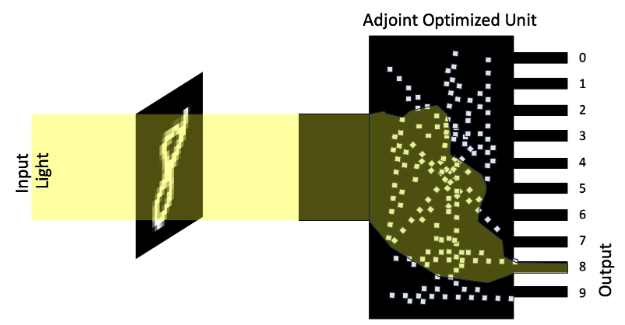
Figure 2. An adjoint-optimized unit for image classification.
MNIST data set can be used to create the diffractors. Free software packages such as “ceviche” [2] or “spins b” [3] can be used to calculate the light propagation through this structure. Note that both solvers are already coupled with adjoint optimizers.
Minimum Requirements:
- Intermediate knowledge of Python (both data structures and algorithms)
- Good understanding of vector calculus
Preferred Skills:
- Familiarity with FDTD or FDFD methods
- Experience in numerical optimization
A.4 Accelerating the Evaluation Sommerfeld Integrals with Machine Learning
Main Research Question: Can we approximately evaluate layered medium Green’s functions, which have highly oscillating and slowly decaying integrands, with machine learning?
Sommerfeld integrals are a set of complex contour integrals that arise in the study of wave propagation and diffraction problems in physics and engineering. The importance of Sommerfeld integrals lies in their ability to provide analytical solutions and insights into complex wave propagation problems. While they can be challenging to evaluate analytically in some cases, they form a foundation for understanding wave phenomena and are often approximated or evaluated numerically when analytical solutions are not feasible.
In this project, we are primarily focusing on layered medium Green’s functions (LMGFs). In electromagnetics, LMGFs (also known as dyadic Green’s functions or tensor Green’s functions) are mathematical tools used to describe and analyze electromagnetic fields in a layered medium. A layered medium refers to a material with distinct regions or layers, each having different electromagnetic properties, such as permittivity and permeability.
For a homogeneous medium, Green’s function is a scalar quantity representing the response of the electric or magnetic field to a point source. However, in a layered medium with different electromagnetic properties at each layer, Green’s function becomes a tensorial quantity, representing the full electromagnetic response with both electric and magnetic fields.
We previously developed a numerical model to evaluate LMGFs and implemented this numerical model in MATLAB. Even though the singularity subtraction technique we developed accelerated the process, we need further improvements to tackle more complicated electromagnetic wave scattering problems. This project aims to achieve this acceleration via machine learning (ML).
Questions that need to be addressed with this research are as follows:
- If we have a large data set, can we predict the LMGFs with ML?
- If the first attempt is not successful, then can we predict the frequency LMGFs with ML and convert them to the spatial domain via numerical integration?
- If either approach works, then what’s the ideal neural network architecture (fully-connected neural networks, recurrent neural networks with attention mechanisms, etc.)?
Note that we already have a MATLAB code to evaluate LMGFs (and hence to create the data set) both in frequency and spatial domains.
Requirements:
- Basic knowledge of MATLAB
- Good understanding of ML algorithms
- Experience in Python programming (especially with Tensorflow-Keras and PyTorch)
References:
[1] Shen, B., Wang, P., Polson, R. et al. An integrated-nanophotonics polarization beamsplitter with 2.4 × 2.4 μm2 footprint. Nature Photon 9, 378–382 (2015).